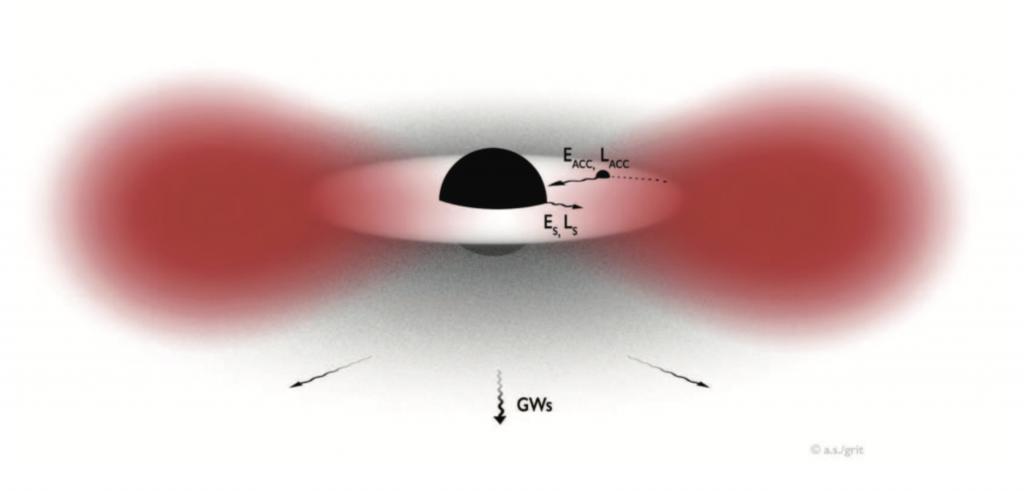
Ultralight boson particles, including scalar (spin 0), vector (spin 1), and tensor (spin 2) fields, have been predicted under several theoretical frameworks to solve problems in particle physics, high-energy theory and cosmology. They could also be a significant component of dark matter. These proposed new particles are difficult to detect by conventional experiments, due to their extremely small mass and weak interaction (if any) with Standard Model particles. Gravitational coupling provides an alternative and promising way to study them. 

Around a rapidly rotating black hole, if there exists a fundamental ultralight boson field, it is expected to grow when the superradiance condition is satisfied: ω < mΩ, where ω is the characteristic angular frequency of a boson, m is the boson azimuthal quantum number with respect to the rotation axis of the black hole, and Ω is the angular speed of the black hole’s outer horizon. When the Compton wavelength of the particle is comparable to the characteristic length of the black hole, the superradiant instability is maximised, and thus the occupation number of ultralight bosons grows exponentially, forming a macroscopic cloud comprising ∼10% of the black hole mass (Fig. 1). 

After the cloud is formed, the bosons in the cloud annihilate into gravitons, generating continuous, quasi-monochromatic gravitational waves over a long lifetime. By searching for these gravitational-wave signals, ground-based detectors (e.g., LIGO, Virgo, and KAGRA), and space-based detectors (e.g., LISA) could be used to probe yet-undiscovered ultralight bosons, which are largely inaccessible to conventional experiments, and constrain their properties.  

At the Centre for Gravitational Astrophysics, we are actively researching the astrophysical sources and signal morphology of gravitational waves from ultralight bosons [2], developing appropriate data analysis methods, and conducting searches in the latest gravitational wave detector data [3]. 

[1] Brito, Cardoso & Pani, Class. Quant. Grav. 32, 134001 (2015) 

[2] Isi, Sun, Brito & Melatos, Phys. Rev. D 99, 084042 (2019) 

[3] Sun, Brito & Isi, Phys, Rev. D 101, 063020 (2020) 

Contacts: Prof Susan Scott, susan.scott@anu.edu.au; Dr Lilli (Ling) Sun, ling.sun@anu.edu.au; Dr Karl Wette, karl.wette@anu.edu.au